To multiply fractions, multiply their numerators and denominators. If the answer is an improper fraction, select the whole part of the fraction.
Example 1. Find the value of the expression 
.
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
The answer is 
. It is desirable to reduce this fraction. Fraction can be reduced by 2. Then the final solution will look like this:
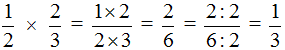
The expression 
can be understood as taking 
of a pizza from half a pizza. Suppose we have half a pizza:
How do you take two thirds of that half? First you have to divide that half into three equal parts:
And take from these three pieces two:
We will have 
of a pizza. Remember what a pizza looks like divided into three parts:
One slice from this pizza and the two slices we took will be the same size:
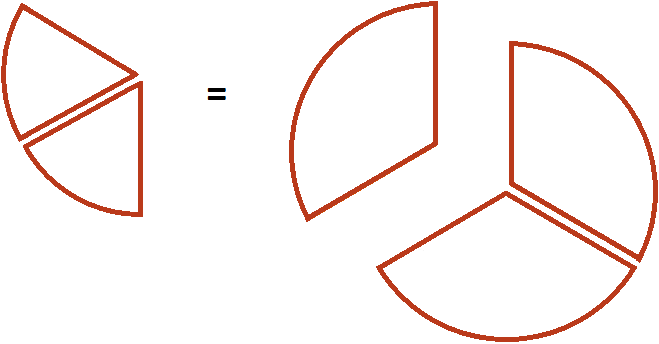
In other words, we are talking about the same size of pizza. Therefore, the value of the expression is
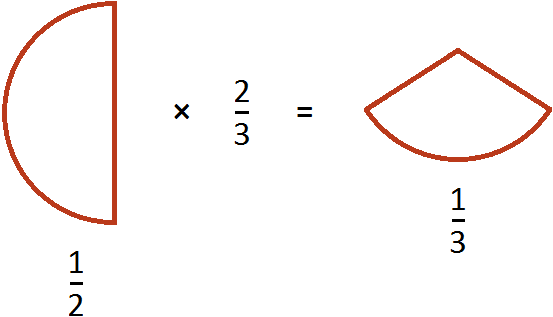
Example 2. Find the value of the expression 
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
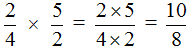
The answer is an incorrect fraction. Let's separate the integer part of the fraction:
Example 3. Find the value of the expression 
Multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
The answer is a correct fraction, but it would be good if it were shortened. To reduce this fraction, divide the numerator and denominator of the fraction by the greatest common divisor (GCD) of the numbers 105 and 450.
So, let's find the GCD of 105 and 450:
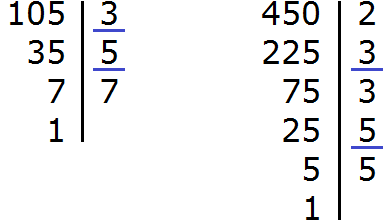
Now divide the numerator and denominator of our answer by the GCD we have now found, that is, by 15
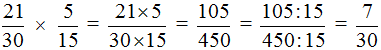
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.