Multiplication of fractions with whole numbers

To multiply a fraction by a number, multiply the numerator of the fraction by that number and leave the denominator unchanged.

Example 1. Multiply a fraction by the number 1.

Multiply the numerator of the fraction by the number 1.

The entry can be understood as taking half 1 time. For example, if you take a pizza once, you get pizzas

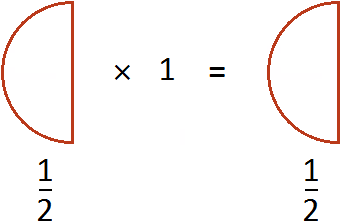
We know from the laws of multiplication that if the multiplier and the factor are swapped, the product will not change. If is written as , then the product is still . Again, the rule of multiplication of a whole number and a fraction is triggered:

This entry can be understood as taking half of one. For example, if there is 1 whole pizza and we take half of it, we have a pizza:

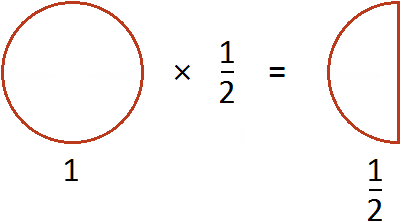
Example 2. Find the value of the expression

Multiply the numerator of the fraction by 4

The answer is an incorrect fraction. Let's separate the integer part of the fraction:

The expression can be understood as taking two quarters four times. For example, if you take of a pizza 4 times, you get two whole pizzas

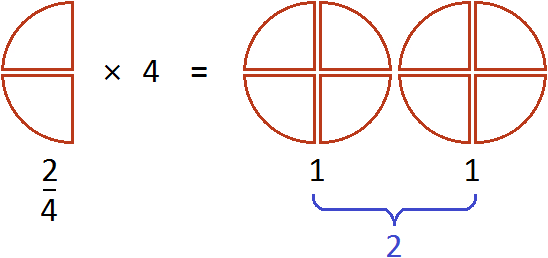
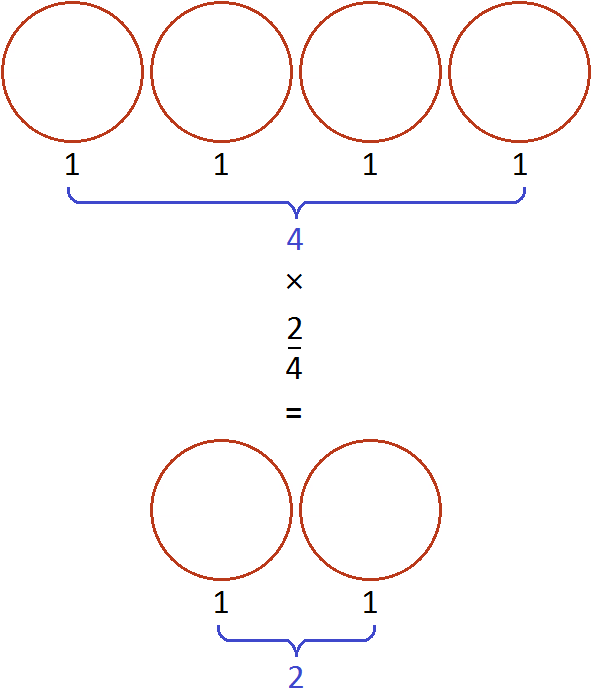
And if we swap the multiplier and the factor, we get the expression . It also equals 2. This expression can be understood as taking two pizzas from four whole pizzas:

The number that is multiplied by a fraction and the denominator of the fraction are allowed to be reduced if they have a common divisor greater than one.

For example, the expression can be calculated in two ways.

First method. Multiply 4 by the numerator of the fraction and leave the denominator unchanged:

The second way. The multiplied foursome and the foursome in the denominator of the fraction , can be reduction. These fours can be reduced by 4, because the greatest common divisor of two fours is the fourself:

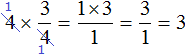
We get the same result 3. After reducing the fours, new numbers are formed in their place: two ones. But multiplying one with three and then dividing by one does not change anything. Therefore, the solution can be written in a shorter form:

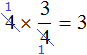
Reduction can be performed even when we choose to use the first method, but at the stage of multiplying the number 4 and the numerator 3 we choose to use reduction:

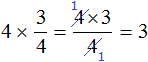
But for example, the expression can only be calculated by the first method - multiplying the number 7 by the numerator of the fraction , and leaving the denominator unchanged:

This is due to the fact that the number 7 and the denominator of the fraction have no common divisor greater than one, and therefore do not reduce.

Some students mistakenly abbreviate the multiplied number and the numerator of a fraction. This should not be done. For example, the following entry is not correct:

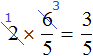
The reduction of a fraction implies that both the numerator and the denominator will be divided by the same number. In the case of 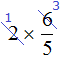, only the numerator is divided, because writing 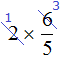is the same as writing 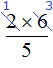. We see that division is performed only in the numerator, and there is no division in the denominator.

Exercises:

Task 1. Find the value of the expression:

Solution:

Show Solution

Task 2. Find the value of the expression:

Solution:

Show Solution

Video lesson

Add comment