Here are short articles answering one specific question.
The rule for dividing a number by a fraction is the same as the rule for dividing a fraction by a number.
To divide a number by a fraction, multiply the number by the fraction inverse of the divisor.
For example, divide the number 1 by ![]() .
.
To divide the number 1 by ![]() , you must multiply the number 1 by the fraction inverse of the fraction
, you must multiply the number 1 by the fraction inverse of the fraction ![]() . And the inverse of fraction
. And the inverse of fraction ![]() is fraction
is fraction ![]() .
.
A decimal, as we know, consists of a whole part and a fractional part. When dividing a decimal by a whole number, the first thing to do is:
- divide the whole part of the decimal by this number;
- after the whole part is divided, you must immediately put a dot in the quotient and continue the calculation as in the usual division.
For example, divide 4.8 by 2
Let's write this example with a corner:
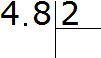
Now divide the whole part by two. Four divided by two is two. Write the two in the quotient and immediately put a dot:
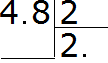
Now multiply the quotient by the divisor and see if there is a remainder of the division:
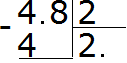
4−4=0. The remainder is zero. Zero is not written down yet, since the solution is not complete. Then continue to calculate, as in the usual division. Write down 8 and divide it by 2
To divide a fraction by a fraction, multiply the first fraction by the fraction inverse of the second fraction.
For example, divide ![]() by
by ![]()
To divide ![]() by
by ![]() , you have to multiply
, you have to multiply ![]() by a fraction that is the inverse of a fraction of
by a fraction that is the inverse of a fraction of ![]() . And the inverse of a fraction
. And the inverse of a fraction ![]() is a fraction
is a fraction ![]()
You may encounter problems in which you need to add a whole number and a fraction. For example, add a number 2 and a fraction![]() . To solve this example, you need to represent the number 2 as a fraction
. To solve this example, you need to represent the number 2 as a fraction ![]() . Then add fractions with different denominators:
. Then add fractions with different denominators:
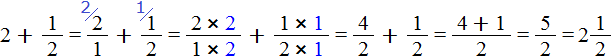
Now look carefully at this example. Let's look at the beginning and the end of it. Its beginning looks like this: ![]() , and the end is this:
, and the end is this: ![]() . The difference is that in the first case the number 2 and the fraction
. The difference is that in the first case the number 2 and the fraction ![]() are joined by an addition sign, and in the second case they are written together. In fact, this is the same thing. The point is that
are joined by an addition sign, and in the second case they are written together. In fact, this is the same thing. The point is that ![]() is a convolute form of a mixed number, and
is a convolute form of a mixed number, and ![]() is an expanded form.
is an expanded form.
When we have a mixed number of the form ![]() in front of us, we must realize that the addition sign is omitted.
in front of us, we must realize that the addition sign is omitted.
To divide mixed numbers, you need to convert them into improper fractions, then do the usual division of fractions. That is, multiply the first fraction by the inversed second fraction.
Example 1. Find the value of the expression ![]()
Let's convert the mixed numbers into improper fractions. We obtain the following expression:
![]()
We already know how to solve this problem. The first fraction ![]() must be multiplied by the inverse of the second fraction. The inverse of the second fraction is fraction
must be multiplied by the inverse of the second fraction. The inverse of the second fraction is fraction ![]() .
.
Let's finish this example to the end:
This topic may seem confusing the first time. Don't despair and give up on learning. Understanding will come in any case. If not immediately, then a little later. The main thing is not to give up and continue to study hard.
In previous examples, we divided a single-digit number by a single-digit number, and this did not give us too much trouble. Now we are going to divide a multi-digit number by a single-digit number.
If you do not understand what single and multi-digit numbers are, we advise you to study the previous lesson, which is called multiplication.
To divide a number that has a zero at the end, you need to temporarily discard that zero, do the usual division, and add that zero to the answer.
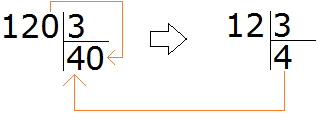
For example, divide 120 : 3
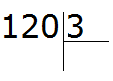
How many threes are there in the number 120? To answer this question, we temporarily discard the zero at the end of 120 and divide 12 by 3 to get 4. Then we add that zero to the quotient. We end up with 40:
In the division lesson we learned how to divide numbers with a remainder. For example, to divide 9 by 5, we did the following:
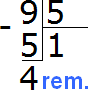
and went on to say that "nine divided by five would be one and four in the remainder".
Now we have the necessary knowledge to divide 9 by 5 without a remainder. Our task is to divide the remainder of 4 into 5 parts. In other words, divide a smaller number by a larger number.
So, let's put a dot after the one in the quotient, indicating that we have finished dividing the whole parts and are moving on to the fractional part:
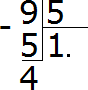
Add zero to the remainder of 4
You may encounter problems that require dividing a whole number by a mixed number. For example, divide 2 by ![]() .
.
To solve this example, convert the divisor ![]() to an improper fraction. Then multiply the number 2 by the fraction inverse of the divisor.
to an improper fraction. Then multiply the number 2 by the fraction inverse of the divisor.
Convert the divisor of ![]() to an improper fraction, you get
to an improper fraction, you get ![]() . Then multiply 2 by the fraction inverse of the fraction
. Then multiply 2 by the fraction inverse of the fraction ![]() . The inverse of fraction
. The inverse of fraction ![]() is fraction
is fraction ![]()
![]()
Let's say there are two whole pizzas:
Definition. Divisibility Rules are used to speed up the process of dividing numbers. There are many signs of divisibility and some interesting algorithms that greatly speed up the solution and free you from unnecessary calculations. Consider the most popular of them.
Divisibility rules by 10
Any number that ends in zero is divisible by 10 without a remainder. To get the quotient, it is enough to discard the number 0 in the divisor.
For example, 380 : 10 = 38. We have simply discarded the last zero in 380.
If we have an expression of this form, 385 : 10, we get 38 and a 5 in the remainder, because 380 : 10 = 38, and a 5 is the remainder that is not divided.
Thus, if the number ends in 0, then it is divided by 10 without a remainder. If it ends in another digit, then it is not divisible by 10 without a remainder. The remainder in this case is equal to the last digit of the number. Indeed, in the example 385 : 10 = 38 (5 in the remainder), the remainder equals the last digit in the number 385, that is, a five.
Definition. An even number is a number that is divisible by 2 without a remainder.
For example, 20 is an even number because it is divisible by 2 without a remainder:
20 : 2 = 10
Definition. An odd number is an odd number if it is divided by 2 and leaves a remainder of 1.
Page 4 of 9