Definition. Divisibility Rules are used to speed up the process of dividing numbers. There are many signs of divisibility and some interesting algorithms that greatly speed up the solution and free you from unnecessary calculations. Consider the most popular of them.
Divisibility rules by 10
Any number that ends in zero is divisible by 10 without a remainder. To get the quotient, it is enough to discard the number 0 in the divisor.
For example, 380 : 10 = 38. We have simply discarded the last zero in 380.
If we have an expression of this form, 385 : 10, we get 38 and a 5 in the remainder, because 380 : 10 = 38, and a 5 is the remainder that is not divided.
Thus, if the number ends in 0, then it is divided by 10 without a remainder. If it ends in another digit, then it is not divisible by 10 without a remainder. The remainder in this case is equal to the last digit of the number. Indeed, in the example 385 : 10 = 38 (5 in the remainder), the remainder equals the last digit in the number 385, that is, a five.
Divisibility rules by 5 and by 2
Any number that ends in zero is divisible without a remainder by both 5 and 2.
Examples:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Divisibility rules by 5
If a number ends in 0 or 5, it is divided by 5 without a remainder.
Examples:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Divisibility rules by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example, consider number 27, the sum of its digits is 2 + 7 = 9. Nine, as we know, is divisible by 3, so 27 is also divisible by 3:
27 : 3 = 9
Divisibility rules by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
For example, consider the number 18. The sum of its digits is 1 + 8 = 9. Nine is divisible by nine, so 18 is divisible by 9.
18 : 9 = 2
Consider the number 846. The sum of its digits is 8 + 4 + 6 = 18. Eighteen is divisible by nine, so 846 is divisible by 9:
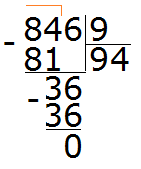
2. If you find an error or inaccuracy, please describe it.
3. Positive feedback is welcome.